BQ #7: Unit V: Derivatives and the Area Problem

Before we dive into where the difference quotient comes from, let's clarify what the difference quotient is and what it is used for. The Difference Quotient just represents a more complex formula to find the slope. It will ultimately help us find the slope of the line that is tangent to any given graph at any point. Because the difference quotient is used to find the slope, it is derived from the slope formula, which is    .

http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png

Please reference the above image to help clarify how the difference quotient is derived. When using the slope formula, we must know the the x and y values. for the first point, the x value is just x. This makes the y value the function of x which is f(x). For the second point, we know that the distance from the first point and second point changes along the x-axis. So this change in x is often represented with a triangle x or "h." This means the x -value for the second point is x +h (or the change in distance along the x-axis). Because the x-value is x+h, this makes the y - value f(x+h). We now have our two points: (x, f(x)) and (x+h, f(x+h)). With that, we can now plug these values into the slope formula leaving us with (f(x+h)-f(x))/(x+h-x). The x's cancel in the denominator leaving us with the difference quotient : (f(x+h)-f(x))/h .


https://www.youtube.com/watch?v=XA0fZh8cXV8

If you are a more visual learner, reference the video above as it colorfully works out step by step how the difference quotient is derived from the slope formula . 

Please note that the difference quotient does not find the slope tangent line to a specific point on the graph, rather, it find the slope of the secant line that can be used to find the derivative. We can find the derivative (or slope of the tangent line) when h approaches 0 because this means the distance between the 2 points decrease until they are one and the same , making it ultimately touch the graph at one point. We can do this by evaluating the as h->0 using direct substitution. I hope this clarifies how the difference quotient is derived and ultimately how it is used to find the derivative.

 

Sources:

 http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png
https://www.youtube.com/watch?v=XA0fZh8cXV8

BQ# 6: Unit U Concepts 1-8: Functions and Their Limits.

1. What is continuity? What is discontinuity?

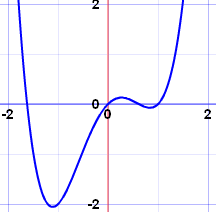
A continuous function is predictable. That means there are no breaks, holes, and jumps. The function can be drawn without lifting the pencil. Here's an example of a continuous function.

http://www.mathsisfun.com/calculus/continuity.html

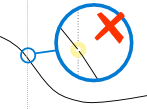
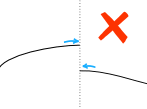
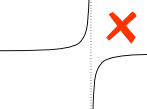
On the other hand, a discontinuous function is unpredictable and may have breaks, holes or jumps. There are two families of discontinuities, removable and non-removable. A point discontinuity is a removable discontinuity known as a hole. For non-removable, there are jump discontinuities, oscillating behavior and infinite discontinuities known as unbounded behavior (it has a vertical asymptote).

http://www.mathsisfun.com/calculus/continuity.html

http://www.mathsisfun.com/calculus/continuity.html

http://www.mathsisfun.com/calculus/continuity.html

The three images above portray 3 different discontinuities, a hole, jump, and infinite discontinuity in which there is an asymptote.

2. What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?

A limit is the height a function intends to reach (y-value). It is read as "The limit as x approaches 'a number' of f(x) is equal to 'L' ". A limit exists as long as you reach the same height from both the left and the right. This means both the left and right limit must be the same. If the graph does not break at a given x-value, then the limit will exist there. This means that a limit will exists in functions with holes. However, a limit will not be reached in non-removable discontinuities such as jumps, oscillating behavior, or infinite discontinuities. For infinite discontinuities, we say the limit is unbounded (or it does not exist) because infinity is not a number. This is because they do not reach the same height from both the left and right side. However, we can still write one-sided limits.While limit is the intended height, the value is the actual height. This means that the limit and value can be the same or different depending on the function. Sometimes, there may be no actual value, as in the case with 2 open circles.

http://www3.ges.sd23.bc.ca/classes/calculus/unit2/U02L02.html

 In the image above, you can see the limit at a is L. However L is not the actual value, it is just the intended height. Instead the value is b, in which there is a closed circle.

3. How do we evaluate limits numerically, graphically, and algebraically?

To evaluate limits numerically, you will have to begin by drawing a table with 3 left and 3 right of number x is approaching. The values on the ends should be a tenth away from the center, and the closer you get to the center, the closer the x-value should be. You would then plug the function into your graphing calculator and trace the location of the x-value. An example can be seen below. However, you should note that the limit as x approaches from the left is 12 while from the right is 4.

x 1.9 1.99 1.999 g(x) 11.41 11.9401 11.9940

2

2.001 2.01 2.1 4.3301 4.3024 4.1039

http://people.hofstra.edu/stefan_waner/realworld/tutorials/frames2_6a.html

To evaluate limits graphically, plug the function into the y= screen on the graphing calculator. Then you can either go to tblset and make the ind. variable ask and then type in the values close to the limit or you can hit trace. To find the limit, put your finger on a spot to the left and to the right of where you want to evaluate the limit and then move them together to find where they meet. If they don't, then there is no limit.


https://www.youtube.com/watch?v=UkjgJQaGx98

Notice in the youtube video above how Patrick in the middle moves his fingers closer and closer to the x-value he wants to approach from both sides. 


When solving for limits algebraically, you need to begin with the method of substitution. Basically, this is taking the number the limit is approaching and plugging it in anywhere you see x. Through substitution, we can get 4 types of answers:
1. a numerical answer- we're done
2. 0/# -this is 0 -we're done
3. #/0 which is undefined and the limit does not exist-we're done
4. 0/0 indeterminate form - use another method
The image below provides a function in which substitution is used to find the limit. 

http://www.onlinemathlearning.com/limits-calculus.html

If we end up with indeterminate form, we can use the dividing out/ factoring method. You factor both the numerator and denominator to cancel out the common terms to remove the 0 in the denominator. Afterwards, you can use substitution with the simplified expression. The image below provides and example of factoring to find the value.

http://www.drcruzan.com/MathLimits.html

If you are unable to factor the function, they you will have to use the rationalizing/conjugate method. First you multiply the top and bottom by the conjugate . Then you simplify by foiling the value that was used to find the conjugate while leaving the other factored. Then there should be something you can cancel so that you can use substitution to find the value.The image below provides an example of multiplying the numerator and denominator by the conjugate, rad(x^2+9)=3 .

http://www.onlinemathlearning.com/limits-calculus.html

References:

http://www.mathsisfun.com/calculus/continuity.html
http://www3.ges.sd23.bc.ca/classes/calculus/unit2/U02L02.html
http://people.hofstra.edu/stefan_waner/realworld/tutorials/frames2_6a.html
https://www.youtube.com/watch?v=UkjgJQaGx98
http://www.drcruzan.com/MathLimits.html
http://www.onlinemathlearning.com/limits-calculus.html

BQ#3 – Unit T Concepts 1-3

How do the graphs of sine and cosine relate to each of the others?  Emphasize asymptotes in your response.

We know that both sin and cos are seen in the ratio identities of the other 4 trig functions. Before examining their relations to each other, we need

Tangent?

The ratio for tangent is sin/cos aka y/x. So the asymptotes are located when tangent is cosine, this would be where cos is equal to 0. Because cos is the x-value, x=0 at pi/2 and 3pi/2this is where the asymptotes are.  Knowing this, we will be looking at the relations between the graphs of tan, cos, and sin. Let's begin with the first quadrant. We know that on the unit circle, Q1 begins at 0 and ends at pi/2. According to ASTC, we know that all trig functions in the first quadrant are positive. However, let's pretend that we don't know that tangent is positive in the first quadrant, how can we find out where tangent belongs? We can use the trig ratio for tan: sin/cos. Both sin and cos are pos. in the first quadrant, when you divide one by the other, you end up with a pos. value for tangent. For Q2, from pi/2 to pi, we know that sin is pos. and cos is neg. This means tangent is neg. in the second Qaudrant because pos/neg=neg. Q3 is from pi to 3pi/2, in which sin and cos are both neg. A neg/neg gives us a pos. value for tan. In Q4, from 3pi/2 to pi, sin is pos and cos is neg. A pos/neg gives us a neg. value for tangent in the 4th quadrant. Thus, the graph for tangent is pos, neg, pos, neg. When we graph it within its period of pi/2 to 3pi/2, the graph will be uphill. In its 1st period, it will start below the x-axis close to the asymptote at pi/2 and move uphill when it enters into Q3 where it is positive. This pattern will continue for every tangent graph. 

https://www.desmos.com/calculator/hjts26gwst

Cotangent?

The trig ratio for cotangent is cos/sin. So the asymptotes are located where sin (y) is equal to 0.Y is equal to 0 at 0 and pi, so this is the location of the asymptotes. We know that on the unit circle, Q1 begins at 0 and ends at pi/2.To find out how the graph for cot looks, we can use the  trig ratio for cot: cos/sin. Both sin and cos are pos. in the first quadrant, so when you divide one by the other, you end up with a pos. value for cot. For Q2, from pi/2 to pi, we know that sin is pos. and cos is neg. This means cot is neg. in the second Quadrant because neg/pos=neg. Q3 is from pi to 3pi/2, sin and cos are both neg. A neg/neg gives us a pos. value for tan. In Q4, from 3pi/2 to pi, sin is pos and cos is neg. A neg./pos. gives us a neg. value for cotangent in the 4th quadrant. Thus, the graph for cotangent is pos, neg, pos, neg. When we graph it within its period of 0 and pi, the graph will begin close to the asymptote above the x-axis.  When it enters Q2 it will be negative so it will start going downhill. This pattern will continue for every cotangent graph.

https://www.desmos.com/calculator/hjts26gwst

Secant?  

The trig ratio for secant is 1/cos. So the asymptotes are located where cos (x) is equal to 0. X is equal to 0 at pi/2 and 3pi/2, so this is the location of the asymptotes. We know that on the unit circle, Q1 begins at 0 and ends at pi/2.To find out how the graph for sec looks like, we can use our knowledge of  trig ratio of sec: 1/cos. Because cos is pos. in the first quadrant, sec is also positive. For Q2, from pi/2 to pi, we know that cos is neg. making sec neg. Q3 is from pi to 3pi/2, in which cos is neg. 1/neg gives us a pos. value for sec. In Q4, from 3pi/2 to pi, cos is pos so sec is also pos. because a 1/pos. gives us a pos. value for secant in the 4th quadrant. Thus, the graph for sec t is pos, neg, neg, pos. Notice that this is the same pattern for cos! When we graph sec, we know that it takes 2pi to have an entire period. Our graph will look like an upside down parabola below the x-axis in Q2 and 3, with he vertex touching with the cos graph. However, in Q4 and 1, the parabola is above the x-axis and shares it vertex with the top of the cos graph.

https://www.desmos.com/calculator/hjts26gwst

Cosecant?

The trig ratio for cosecant is 1/sin. So the asymptotes are located where sin (y) is equal to 0. Y is equal to 0 at 0 and pi, so this is the location of the asymptotes. We know that on the unit circle, Q1 begins at 0 and ends at pi/2.To find out how the graph for csc looks like, we can use our knowledge of  trig ratio of csc: 1/sin. Because sin is pos. in the first quadrant, csc is also positive. For Q2, from pi/2 to pi, we know that sin is pos. making csc pos. Q3 is from pi to 3pi/2, because sin is neg. 1/neg gives us a pos. value for csc. In Q4, from 3pi/2 to pi, sin is neg so 1/neg. gives us a neg. value for csc in the 4th quadrant. Thus, the graph for csc is pos, pos, neg, neg. Notice that this is the same pattern for sin and csc! When we graph it withing Q1 and 2, the graph will look like a parabola above the x-axis in which it shares its vertex with the sin graph.  When it enters Q3 and 4 it will look like an upside down parabola below the x-axis, sharing its vertex with sin as well.

https://www.desmos.com/calculator/hjts26gwst

BQ#4 – Unit T Concept 3

Why is a “normal” tangent graph uphill, but a “normal” tangent graph downhill? Use unit circle ratios to explain.

We know that the ratio for tangent is y/x. This means the asymptote is where x is equal to 0 (making the ratio undefined). The x-value is equal to O at (0,1) and (0,-1) which is pi/2 and 3pi/2, which could also be referred to as -pi/2. When we draw these asymptotes located at pi/2 and -pi/2 on a graph, the period consists of Q4 and Q1. According to ASTC, Tan is negative in Q4 and positive in Q1. Because of this, the only possible way to draw this is with an uphill graph. It will begin below the x-axis in Q4 and then move above the x-axis when it enters into Q1. For cot, which is x/y, the asymptote is where y is equal to 0. This occurs at (1,0) and (-1,0), which is 0 and pi. When we draw the asymptotes, the period consists of Q1 and Q2. Because cot is pos. in Q1 and neg. in Q2, the shift is from pos to neg. The only way to draw this downhill. The cot graph will begin near the asymptote above the x-axis and then go downhill to below the x-axis when it reaches Q2. Through this reasoning, a normal tangent graph is uphill while a normal cotangent graph is downhill. 

 The image below will help clarify the difference between tan and cot in reference to uphill or downhill.

BQ#5 – Unit T Concepts 1-3

Why do sine and cosine NOT have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

In order for a trig function to have an asymptote, it must be undefined. We know that the ratio for sin is y/r and the ratio for cos is x/r. In a unit circle, the measure of r will always equal 1, thus, the value of sin and cos will never be undefined. As a result, there are no asymptotes. However the other trig functions do have asymptotes. Let's look at why this is. Cosecant has asymptotes where sine is equal to 0.This is because it is the reciprocal of sine, 1/sin. This means that when the value of y is 0, the value of cosecant is 1/0, making it undefined. Similarly, Cotangent has an asymptote when sin = 0 (y=0) because it's trig ratio is cos/sin. Because both cosecant and cotangents asymptote depend on when y = 0, they share the same asymptotes at (1,0) and (-1,0) which would be 0* and 180*, also referred to as 0 and pi in radians (the 2 points on the unit circle where the y values are 0). Secant is undefined when cos is equal to 0 (x=0). The value of secant would be 1/0 , making it undefined. Likewise, tangent is y/x , so whenever the x value= 0 , there is an asymptote. The x-value equals 0 at (0,1) and (0,-1) which can also be written as pi/2 and 3pi/2. Because of this, secant and tangent share the same asymptotes, both relying on their denominator of x. 

Please refer to the picture below that identifies the different unit circle ratios.

BQ#2 – Unit T Concept Intro

How do the trig graphs relate to the Unit Circle?

When you straighten out the unit circle, it is easier to decipher how it is related to trig graphs. With our former knowledge of trig functions, we know that each trig function has its positive and negative values, depending on which quadrant it is located in. According to ASTC, we know that sine is positive in the first and second quadrant and negative in the third and fourth(+ + - -). We can take what we know from the unit circle and use it to help graph our trig functions by even using the points on the unit circle ( 0, pi/2, pi, 3pi/2, 2pi). Because sin is positive in the first and second quadrant, this part of the graph will be above the x-axis (the distance from 0-pi). Likewise, the part of the unit circle in the third and fourth quadrant will be in the negatives, below the x-axis(the distance from pi-2pi). Similarly to the unit circle, trig graphs can also be divided into "quadrants". For Cosine, it is positive in the first and fourth quadrant and negative in the second and third quadrant(+ - - +). As a result, when a cosine graph is plotted, it will be above the x-axis for the first quadrant, below the x-axis for quadrant 2 and 3 because it is negative. Then it rises above the x-axis again when it enters quadrant 4. for Tangent/Cotangent, it is positive in the 1st, negative in the 2nd, positive in the 3rd, and negative in the 4th. The pattern is basically + - + -. So when graphing , quadrant 1 and 3 will be above the x-axis while 2 and 4 will be below.

Please Refer to this picture as you read through the text to help clarify on what I mean by the Quadrants and how it ultimately affects the graph. Additionally, a sketch of a sin, cos, and tan graph are provided in relation to the quadrants.

a) Period?

To understand why the period for sin and cos is 2pi, we must define a period. A period is one time through the cycle, one repeat of the pattern as you can say. When looking at a sin graph, we know that it is above the x-axis for the first 2 quadrants (from 0 to pi) and below for the last 2 quadrants (from pi to 2 pi). Thus the pattern is pos-pos-neg-neg, from 0 to 2pi. As a result, one repetition requires 2pi. Similarly, the pattern for cosine can be described as beginning positive from 0, once it reaches pi/2 the graph remains negative until reaching 3pi/2. From there it enters the fourth quadrant in which it is positive to the point 2pi. As a result the pattern can be simplified to pos-neg-neg-pos.This means that cos also requires 2pi for a period. However, tangent shifts from being positive beginning at 0 - pi/2. then it becomes negative from pi/2 - pi. From there, it becomes positive once again till it reaches 3pi/2. Then it becomes negative till 2pi. Thus the pattern is pos-neg-pos-neg. However, we see that the pattern repeats itself twice within one unit circle. Thus, one period will only need to be half of the unit circle which is pi.

b) Amplitude?

Sine and Cosine have amplitudes because they are restricted to values ranging from -1 to1. We know that sin is y/r and cos is x/r. R can only be one because the radius of a unit circle is always 1. Because the radius is 1, the y and x values can not go beyond 1 meaning it has to be equal to or less than 1 or negative 1. When dividing the max value for y , which is one, by r, which has to be one, the greatest value we can have is 1. For these reasons, there are asymptotes, restricting the functions. As for the other trig functions, there are no amplitudes because there are no restrictions based on their ratios. For example, csc is 1/sin. The value of sine can range from -1 to 1. If the value was 0.1, then if we divide 1 by 0.1 we get 10. For these reasons, csc can't be restricted. The following applies to the rest of the trig functions. Tan is sin/cos, and the value of cos can range from 1 to -1. Thus we have an unrestricted value for tangent. This is the reasoning behind why there are limits on sin and cos but no restrictions for the others.

Reflection#1: Unit Q: Verifying Trig Identities

1. What does it actually mean to verify a trig identity?

 Verifying a trig function means to prove that one side is equal to the other side, to prove that it is true. This can be accomplished through manipulating one side of the equation to make it look like what we want it to. This is usually making the left side look like the right side of the equations. To verify, identities are used to simplify the equation as much as possible in order to get to the point we want them to be.

2. What tips and tricks have you found helpful?

 Since there are no set steps to verifying trig functions, it can be a bit confusing, like a puzzle. However, the biggest tip I have, is to practice, practice, practice! This is a concept that takes a lot of practice problems in order to improve. Practice is very beneficial in the fact that it helps you memorize the identities as well as recognize patterns. Depending on how the problem is formatted, different approaches need to be taken. Although there are no set ways to approach a problem, there are indeed patterns that are useful when recognized.

3.Explain your thought process and steps you take in verifying a trig identity.  Do not use a specific example, but speak in general terms of what you would do no matter what they give you. 

When I first begin verifying a trig functions, I check to see if I have solved a similar problem before hand. If it is entirely new, there are a couple approaches that I find useful. When I am stuck, I find it helpful to look for the greatest common denominator. If there is none, I check to see if I can substitute for and identify or if changing everything to sin and cos. If this is not possible, I check if multiplying a conjugate will be helpful. If all these are not useful, I use  various other simplification methods that include combining fractions with a binomial denominator, separating fractions with monomial denominators, or factoring. 

SP#7: Unit Q Concept 2: Finding All Trig Functions When Given One Trig fFunction and Quadrant

This SP7 was made in collaboration with Mason Nguyen.  Please visit the other awesome posts on their blog by going here

Using Identities

Using SOHCAHTOA

 The viewer must pay special attention to identifying which quadrant the triangle is in. This is crucial because it determines which trig functions will be positive and which ones will be negative. Additionally, it is important to pay attention to the denominator, there cannot be a radical in the denominator, it must be rationalized. Lastly, the viewer should be able to recognize that the trig functions were solved in two ways, through the use of identities and  SohCahToa, these two methods resulted in the same correct answers! :)

I/D3: Unit Q - Pythagorean Identities

INQUIRY ACTIVITY SUMMARY:

1. To understand where sin^2x+cos^2x=1 comes from, we must understand that what an identity is. An identity is a proven fact and formula that are always true. The Pythagorean Theorem is an identity because it meets these requirements. The Pythagorean Theorem is a^2+b^2=c^2. However, it can also be re-written as x^2+y^2=r^2. This is because when we look at a triangle in the unit circle, the horizontal leg is x, the vertical leg is y and the length of the hypotenuse is referred to as r. To further simplify the theorem, we want it to equal to one. To accomplish this, we will have to divide both sides of the equation by r^2, because r^2/r^2 is equal to 1. After completing this step, we are left with (x/r)^2+(y/r)^2=1. Isn't this beginning to look very similar? Because we know the unit circle, we know that cosine on it is x/r. We also know that the ratio for sine is y/r. Knowing this we can substitute Cos^2x and Sin^2x for (x/r)^2 and (y/r)^2 in the equation. We are now left with Cos^2x + Sin^2x=1. Now, we can understand that  Cos^2x + Sin^2x=1 is referred to as a Pythagorean Identity because it is both derived from the Pythagorean theorem and is also a formula that always proves true.

Let's choose 30* for on of the magic 3 ordered pairs from the unit circle to prove this identity true. We know  the ordered pair is (rad3/2, 1/2). We can plug rad3/2 in for cos^2x because cosine is x/r. We can also plug in 1/2 for sin^2x because sine is y/r. When we square both of these, we end up with 3/4+1/4 and this is equal to one, which simplifies to 1=1, proving this identity true.

2. From sin^2x+cos^2x=1, we can divide the entire equation by cos^2x. This leaves us with (sin^2x/cos^2x)+(cos^2x/cos^2x)=(1/cos^2x). Using our ratio identities, we know that (sin^2x/cos^2x) is equal to tan^2x, (cos^2x/cos^2x) is equal to 1, and (1/cos^2x) is equal to sec^2x. We can now rewrite our new equation as tan^2+1=sec^2x.

Additionally, we can divide the entire equation by sin^2x. This leaves us with (sin^2x/sin^2x)+(cos^2x/sin^2x)=(1/sin^2x). Using our knowledge or ratio identities, we know that (sin^2x/sin^2x) is equal to 1, (cos^2x/sin^2x) is equal to cot^2x, and (1/sin^2x) is equal to csc^2x.We can rewrite this new equation as 1+cot^2x=csc^2x.

INQUIRY ACTIVITY REFLECTION:

1. “The connections that I see between Units N, O, P, and Q so far are…” that all triangles are interconnected with the unit circle's right triangles and that the ratios derived can be used to solve for non-right triangles as well. 2. “If I had to describe trigonometry in THREE words, they would be…” Relationships involving triangles!

BQ# 1: Unit P Concept 1-5: Law of Sines and Area of an Oblique Triangle

1. Law of Sines: 

Why do we need it?Because most triangles are not right triangles, we must find the sides or angles of a triangle using a different method (Sorry Pythagorean Theorem). In the case that we are given Angle-Angle-Side (AAS) or Angle-Side-Angle (ASA), we can use the law of Sines.

Here is an image of a non-right triangle, labeled A B C for the angles and a b c for the sides.

http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm

 If we drop down a perpendicular line from angle C, we form 2 right triangles. Let's label the line h.

http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm

 

Recall that the area of a triangle is Area=1/2bh. In order to find the area, we need to find h, the height. From past concepts with right triangles, we know that Sin A = h/b and that Sin B=h/a. To get h by itself, we will multiply the first equation by b and the second by a. The resulting equations would be bSinA=h and aSinB=h. Because both equations are equal to h, we can use the transitive property to have the equations equal each other: bSinA=aSinB. To simplify, we can divide everything by ab to get SinA/a=SinB/b.

http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm

 

We can prove this again by drawing a perpendicular line from Angle A. We now have Sin B=h/c and
Sin C=h/b. We can rewrite both as cSinB=h and bSinC=h. Using the transitive property we have
cSinB = bSinC. By dividing both by bc, we end up with SinB/b and SinC/c. Since SinB/b is equal to SinA/a as formally proved, we can set all of these rations equal to each other. This gives us the law of Sines which is
.

4. Area Formulas:

How is the “area of an oblique” triangle derived?
Recall that the area of a triangle is A=1/2bh. If we need to find the area of a triangle but we don't know what the height is, we can do it using the area of an oblique triangle.

http://www.compuhigh.com/demo/lesson07_files/oblique.gif

In the image above, we know that SinC is equal to h/a. If we multiply both sides by a we get aSinC=h. If we substitute this value for h into the area of a triangle formula, we get : A=1/2b(aSinC). We can find the area given different information as well. If given side b and c, we need to know angle A, if given side a and c, we need to know Angle B. Similarly to how we solved for the area of the triangle using angle C earlier, we can do the same for angle A and B. Ultimately, we end up with the formula :

http://wps.prenhall.com/wps/media/objects/551/564474/StudyGuide/7c1h7_1.gif

 

 

 

 

 

 

How does this relate to the area formula you are familiar with? This relates to the area formula because it is used in deriving the are of an oblique triangle. We basically used sine to find the value of the height and substituted the formula into the equation. Ultimately, the area formula is still being used, it just looks different .   

 

                                                                       References:

http://wps.prenhall.com/wps/media/objects/551/564474/StudyGuide/7c1h7_1.gif

 

 

 

 

                                      http://www.compuhigh.com/demo/lesson07_files/oblique.gif

http://math.ucsd.edu/~wgarner/math4c/derivations/trigidentities/lawofsines.htm

 

 

WPP #13-14: Unit P Concept 6 & 7: Applications with Law of Sines and Cosines

This WPP13-14 was made in collaboration with Jade Hang.  Please visit the other awesome posts on their blog by going here

Create your own Playlist on LessonPaths!

WPP #12: Unit O Concept 10: Solving Angle of Elevation and Depression

Create your own Playlist on LessonPaths!

I/D #2: Unit O-How can we derive the patterns for our special right triangles?

INQUIRY ACTIVITY SUMMARY

1. 30-60-90 triangle: We are given an equilateral triangle with a side length of 1. I drew a vertical line straight down the center of the equilateral triangle to get 2 30-60-90 triangles.

 If I look at one of the triangles, I know that the hypotenuse (the side across from the 90* angle) is 1 and the shortest side is 1/2 because we cut the side in half. To find the height , opposite of the 60* angle, I used the Pythagorean theorem, a^2+b^2=c^2.

 I plugged in 1/2 for a  and 1 for c. Squaring 1/2 gave me 1/4 and squaring 1 is 1. I wanted to solve for b^2 so i subtracted 1/4 from both sides, giving me 3/4. Next, I took the square root of both sides, leaving me with b=rad3/2. To translate this into a normal pattern( without fractions, I multiplied all the side lengths by 2. This gave me a hypotenuse of 2, the shortest leg was 1 and the height was rad3. 

Lastly, I added n to all of the side lengths. This is so that this concept can be applied to all 30-60-90 triangles. By adding n, we emphasize the relationship between the sides, so that we can still solve for sides with different values (not just one) by applying the ratio.

2.  45-45-90 triangle: When given a square with a side length of 1, we can derive the patterns for this special right triangle. First, I drew a diagonal line connecting 2 opposite angles to form 2 45-45-90 degree triangles.

 Knowing the length of 2 of the sides, which is 1, I used the Pythagorean Theorem (a^2+b^2=c^2) to solve for the hypotenuse. I plugged 1 into a and 1 into b. First I squared them giving me 1+1=c^2 -> 2=c^2. Next, I took the square root of both sides to give me the hypotenuse of rad2.

 Now that I have the length for all 3 sides, I added n to each of the lengths so that it can apply to all 45-45-90 triangles when the side length is not 1. Through using this ratio, the relationship of the 45-45-90 degree angles will remain constant with the measure of the sides.

INQUIRY ACTIVITY REFLECTION

1. Something I never noticed before about special right triangles is how the ratios came to be. I never realized that the ratios came from the Pythagorean theorem!
2. Being able to derive these triangles myself aids in my learning because I now conceptually understand the roots of the rules of special right triangles. Through this activity, I am not simply memorizing information, because I now understand where these values came from. Even if I forget the ratios, I will be able to derive these patterns.

I/D# 1: Unit N Concept 7: How do SRT and UC relate?

INQUIRY ACTIVITY SUMMARY

1.        Describe the 30* triangle: The first thing I did was label according to the rules of the special right triangles. For the the 30* triangles, the hypotenuse is 2x, the opposite side is x, and the adjacent angle is xrad3. To simplify the 3 sides so that the hypotenuse is 1, 2x was divided by 2x to give me one. Since I divided the hypotenuse by 2x, I would have to divide the other two sides as well. The opposite side would be x divided by 2x, giving me 1/2. The adjacent side would be xrad3 divided by 2x to give me rad3/2. Next, I labeled the hypotenuse r, the horizontal value x and the vertical value y.

          I then drew a coordinate plane so that the origin is located at the labeled angle measure. The next step is to find the ordered pairs. The labeled angle is at the origin, so the ordered pair is (0,0). When looking at the 90* angle, we can see that the length of the x-side is rad3/2 and it lies on the x axis (the y -value is 0). This means the ordered pair would be (rad3/2, 0). Looking at the 60* angle, we notice that it the point is rad3/2 distance right of the origin and 1/2 distance above the origin, giving it the ordered pair (rad3/2, 1/2).

2.        Describe the 45* triangle: I labeled the triangle according to the rules of special right triangles. For the 45* triangle, the hypotenuse is xrad2, the horizontal side is x, and the vertical side is x as well. To make the hypotenuse 1, I divided xrad2 by xrad2 to give me one. Now I have to divide the two other sides by xrad2 as well. Since both are x, when I divide by xrad2, I get rad2/2. Then label the hypotenuse r, the horizontal value x and the vertical value y.

           Since the labeled angle, 45* is at the origin, the ordered pair is (0,0). The length of the x-side is rad2/2 and the point lies on the x-axis. This means the ordered pair would be (rad2/2, 0). Because the angle made from the hypotenuse and opposite side is rad2/2 right of the origin and the length or the vertical side is rad2/2,   the ordered pair would be (rad2/2, rad2/2).

3.        Describe the 60* triangle: This is very similar to the 30* triangle except the angles are flipped. The first thing I did was label according to the rules of the special right triangles. For the the 60* triangles, the hypotenuse is 2x, the opposite side is xrad3, and the adjacent angle is x. To simplify the 3 sides so that the hypotenuse is 1, 2x was divided by 2x to give me one. Since I divided the hypotenuse by 2x, I would have to divide the other two sides as well. The opposite side would be xrad3 divided by 2x, giving me rad3/2. The adjacent side would be x divided by 2x to give me 1/2. Next, I labeled the hypotenuse r, the horizontal value x and the vertical value y.

          I then drew a coordinate plane so that the origin is located at the labeled angle measure (60*). The next step is to find the ordered pairs. The labeled angle, 60*, is at the origin, so the ordered pair is (0,0). When looking at the 90* angle, we can see that the length of the x-side is 1/2 and it lies on the x axis (the y -value is 0). This means the ordered pair would be (1/2, 0). Looking at the 30* angle, we notice that it the point is 1/2 distance right of the origin and rad3/2 distance above the origin, giving it the ordered pair (1/2, rad3/2).

4.This activity helps us derive the UC by enabling us to understand the reasons to the values of certain points on the circle. The points on a unit circle is made from 30*, 45*, and 90* angles that are seen throughout all of the 4 quadrants. We now understand where the ordered pairs come from. Through simplifying the 3 sides of the triangle to make the hypotenuse equal to one, I was able to find the length of all three sides in proportion to each other. With this, I was able to find the 3 ordered pairs of the triangle. For all three triangles, the point formed from the joining of the hypotenuse and opposite angle represents a point on the unit circle. For the 30*, 45*, and 90* triangles, the ordered pairs of the previously explained point are (rad3/2, 1/2) (rad2/2, rad2,2) and (1/2, rad3/2). These three ordered pairs are repeatedly seen in all three quadrants. 
If you draw right triangles connecting the ordered pair to the origin on a unit circle, these triangles are identical to the triangles we encountered with this activity. Because of this activity, we now know where the ordered pairs come from, rather than just memorizing the graph, we are now able to explain why it is this certain way. We can also explain why the point at 0* is (1,0), the ordered pair at 90* is (0,1), at 180* is (-1,0), and the ordered pair at 270* is (0, -1) because the radius is 1.

 
5. The triangle in this activity lies in the first quadrant. The values of the the ordered pairs change as you draw it in the other 3 quadrants. For quadrant 2, all of the x values will be negative because it lies to the left of the origin. For quadrant 3, the x and y values will both become negative because the triangle lies to the left of the y axis and below the x axis. Only the y values will be negative in quadrant 4 because the triangles is below the x axis. 

This is a 30* triangle in Quadrant 2, note that the all x-values are negative.

This is a 45* triangle in Quadrant 3, note that both the x and y values are negative.

This is a 60* triangle in Quadrant 4, note that all the y-values are negative. 

INQUIRY ACTIVITY REFLECTION

1. The coolest thing I learned from this activity was how all the 4 quadrants follow the same patterns of special triangles, the only difference is that some are negative.

2. This activity will help me in this unit because I now understand where the values of the Unit Circle comes from, that the numbers are not random, and that you can find them using special right triangles.

3. Something I never realized before about special right triangles and the unit circle is how they are interconnected. I never noticed that you could be able to draw these special right triangles with in the Unit Circle and have the ordered pairs the same.