BQ #7: Unit V: Derivatives and the Area Problem

Before we dive into where the difference quotient comes from, let's clarify what the difference quotient is and what it is used for. The Difference Quotient just represents a more complex formula to find the slope. It will ultimately help us find the slope of the line that is tangent to any given graph at any point. Because the difference quotient is used to find the slope, it is derived from the slope formula, which is    .

http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png

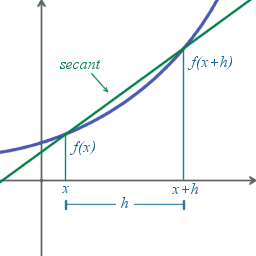
Please reference the above image to help clarify how the difference quotient is derived. When using the slope formula, we must know the the x and y values. for the first point, the x value is just x. This makes the y value the function of x which is f(x). For the second point, we know that the distance from the first point and second point changes along the x-axis. So this change in x is often represented with a triangle x or "h." This means the x -value for the second point is x +h (or the change in distance along the x-axis). Because the x-value is x+h, this makes the y - value f(x+h). We now have our two points: (x, f(x)) and (x+h, f(x+h)). With that, we can now plug these values into the slope formula leaving us with (f(x+h)-f(x))/(x+h-x). The x's cancel in the denominator leaving us with the difference quotient : (f(x+h)-f(x))/h .


https://www.youtube.com/watch?v=XA0fZh8cXV8

If you are a more visual learner, reference the video above as it colorfully works out step by step how the difference quotient is derived from the slope formula . 

Please note that the difference quotient does not find the slope tangent line to a specific point on the graph, rather, it find the slope of the secant line that can be used to find the derivative. We can find the derivative (or slope of the tangent line) when h approaches 0 because this means the distance between the 2 points decrease until they are one and the same , making it ultimately touch the graph at one point. We can do this by evaluating the as h->0 using direct substitution. I hope this clarifies how the difference quotient is derived and ultimately how it is used to find the derivative.

 

Sources:

 http://upload.wikimedia.org/wikipedia/commons/8/8c/Derivative.png
https://www.youtube.com/watch?v=XA0fZh8cXV8