2. The equation for ellipses is
. Graphically, an ellipse looks like a stretched out or elongated circle, it is oval shaped. Key features of ellipses include the center, major axis, minor axis, vertices, co-vertices, foci, and eccentricity. Graphically, the center is a point inside the ellipse which is the intersection of the major and minor axes, h,k. The next paragraph will go over the description of these key terms and on how to identify them graphically and mathematically. 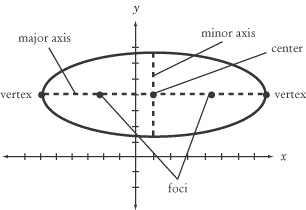You can find these points algebraically by looking at the standard form of the ellipse. The x value will always be h and the y value will always be k, giving the center the point (h,k). "The major axis is the longest diameter of the ellipse."(http://www.mathopenref.com/ellipse.html) To determine if the major axis is horizontal or vertical , look at the standard form. It is horizontal if the bigger denominator is under the x^2 term and this means the ellipse will be fat. It will be vertical if the bigger denominator is under the y^2 term and the ellipse will be skinny. Algebraically, the bigger denominator is the a^2 term and the smaller, b^2. The major axis will be represented by a solid line and the length is 2a. Graphically, the minor axis is the shortest and is perpendicular to the major axis. This axis is represented by a dotted line. Algebraically, the length of the minor axis is 2b, meaning b distance from the center. Vertices are the points at the end of the major axis. To find this, plot a units to the left and right if x^2 has the bigger value under it. Plot it a units up or down if Y^2 has the bigger number under it. The vertices are expressed as 2 points that lie on the major axis.Co-vertices are the points at the end of the minor axis. You can plot the co-vertices b units up and down if x^2 has the bigger value under it or left and right if the Y^2 value has the bigger number under it. You can draw the ellipse by connecting all four points. The foci are the 2 points that define the ellipse. The closer the foci is to the center, the more circular the ellipse will be. The farther away the foci is from the center , the more it deviates from a circle, meaning its more stretched out. this gives it an eccentricity closer to 1. To plot the foci, plot c units to the left and right if x^2 has the bigger value under it. Plot it c units up and down if Y^2 has the bigger number under it. To find any missing values, use the formula: c^2=a^2-b^2. Eccentricity is the measure of how much the conic section deviates from being circular. For ellipses, the eccentricity is between 0 and 1. You can find this by dividing c by a.
People think that most objects in space that orbit something else move in circles, but that isn't the case. Although some objects follow circular orbits, most orbits are shaped more like stretched out circles/ovals. Mathematicians and astronomers refer to this oval shape as an ellipse. All of the planets in our solar system, satellites, and most moons have elliptical orbits.
Earth moves around the sun in an elliptical orbit. Earth's orbit is almost a perfect circle! its eccentricity is only 0.0167 which is very close to that of a circle, 0. Pluto has the least circular orbit of any of the planets in our Solar System (maybe because its not a planet! LOL). Pluto's orbit has an eccentricity of 0.2488. The Sun isn't quite at the center of a planet's elliptical orbit, instead, the sun is at the focus of the ellipse. "Because the Sun is at the focus, not the center, of the ellipse, the planet moves closer to and further away from the Sun every orbit." (http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html)
4. References:
http://cseligman.com/text/history/ellipses.htm
http://www.mathopenref.com/ellipse.html
http://www.windows2universe.org/physical_science/physics/mechanics/orbit/ellipse.html
http://www.youtube.com/watch?v=5nxT6LQhXLM
No comments:
Post a Comment